特報4)東日本大震災の前震と余震の発震機構オイラー回転による判別
2014年12月20日 発行
1.発震機構オイラー回転
地震の発震機構の変化を定量的に検討するために,発震機構回転角の算出法を考案し,東日本大震災の本震域で起こった地震の発震機構がどのような変遷を辿ったかを解析した.
解析に使用したのは,気象庁がホームページで公開している,東日本大震災本震域で2011年に起こった地震のCMT発震機構解である.
発震機構解の圧縮主応力P軸・引張主応力T軸・中間主応力N軸方位について,対応する地震のPT・TN・NPの3組の主応力軸方位対を同時に一致させるオイラー回転極と回転角を算出できる(速報58). 対応する地震について3組の回転極と回転角が算出されるが,算出に用いた二つの主応力軸について算出される回転角の差が最小となる回転極と回転角を採用した(図142).最小回転角差は0.1°程度である.
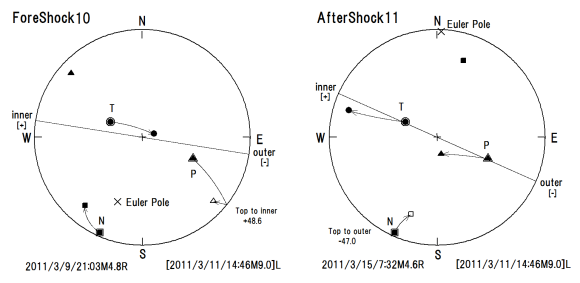
図142.発震機構回転極と主応力軸方位との関係.
下半球方位として与えられているP軸を親指,T軸を人差し指,N軸を中指とすると,基準の本震(Main Shock)は左手系Lであるが,2011年3月9日21時3分M4.8の第10前震(ForeShock)は右手系Rであるので,左手系に変換するためにP軸について上半球方位を用いて,発震機構回転極を算出する.基準の主応力軸をEuler回転極(201+25)の小円に沿って同じ角度(48.6°)回転させると第10前震の主応力軸と一致する.P軸の回転は上半球に入ると左方へ回転し,座標頂(Top)が島弧側(inner)に回転するので,回転角符号は正と判定できる(左図).
2011年3月15日7時32分M4.6の第11余震も右手系Rであり,N軸に上半球方位を使用して手系を合致させる.基準(本震)の主応力軸をEuler回転極(2+1)の回りに47.0°回転すると余震の主応力軸と一致する.N軸の回転は上半球に入ると右方へ回転し,座標頂が海溝側(outer)に回転するので,回転角符号を負と判定できる(右図).
黒塗り潰し:下半球,白抜き:上半球,二重:基準(本震)
△:圧縮主応力P軸,○:引張主応力T軸,□:中間主応力N軸.×:発震機構オイラー回転極方位(下半球).大円:海溝軸に直交する小円方位.等角投影.
算出された回転極の方位が,海溝軸方位に直交する線よりも南側を向けば,発震機構座標の上方軸(座標頂)が島弧側へ回転し,北側を向けば海溝側へ回転したことになる.島弧側への回転を「正」,海溝側への回転を「負」と,符号を付けて発震機構回転角に回転極性も表現できるように定義する.地震の位置する小円区の小円方位は海溝軸方位に直交する方位であるので,回転極性判定に小円方位を使用する.
2.東日本大震災本震域地震の本震基準の発震機構回転角
本震の発震機構を基準に,本震域で2011年に起こった地震の発震機構回転角を算出した.本震が基準なので本震の発震機構回転角は0となるが,2月16日から開始して本震直前まで続いた18個の前震は全て正回転角であるのに対し,本震後の35個の余震は負回転角であることが判明した(図143).発震機構回転角符号が本震を境に前震と余震で急変することは,それまで蓄積されてきた歪が本震によって解放されたことに対応する.
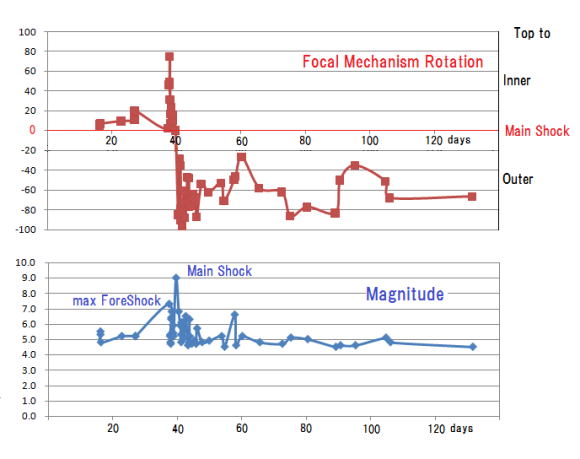
図143.東日本大震災本震を基準にした前震と余震の発震機構回転角.
本震(Main Shock)を基準にした発震機構回転は,2月16日から開始した前震18個が全て島弧側(Inner:正)への回転であるのに,3月11日の本震以後の余震35個は海溝側(Outer:負)への回転へと逆転している.3月9日の最大前震(max ForeShock
)以後も本震まで正であり,余震と区別できる.
横軸:2011年2月1日からの日数.縦軸(上):発震機構回転角(座標頂が島弧側(Inner)への回転が正;海溝側(Outer)への回転が負),縦軸(下):マグニチュード.
3.前震であった2011年3月9日の地震M7.3
3月9日の最大前震M7.3の本震誤認が防災対策に深刻な影響を与えたが,発震機構回転角の符号に基づけば,前震と判定でき,本震が近付いていると予報可能であった.最大前震が前震であることは,翌3月10日の地震の発震機構回転角絶対値がそれまでの前震と同様に25°以内に収まっていることから,本ホームページでは前震と判定してきたが(速報29),符号付き発震機構回転角を用いれば容易に判別できることが明らかになった.ちなみに,最大前震の発震機構回転角は+3.9°と本震の発震機構と殆ど同じであり,余震の発震機構回転角の絶対値は25°以上である.
4.発震機構回転角と地震予報
東日本大震災本震を基準に本震域で起こった地震について算出した発震機構回転符号によって本震前の前震と本震後の余震が区別できることが明らかになった.
気象庁は発震機構解(速報値)を地震発生の1日以内に公表している.この発震機構解の発震機構回転角を算出すれば,震源域で進行している応力場変動を監視でき,地震予報に役立つであろう.特に本震前の前震と本震後の余震の判定は,防災上最も重要な「これから本震が起こる」のか,「本震が起こったので地震活動は終息に向かう」のかに直結し,地震予報における最も重要な課題である.
本ホームページでは地震予報に役立てるため,今後日本列島域で起こる地震について定常的に発震機構回転角を解析する.
注1]発震機構手系の変換
気象庁公表の発震機構解は,下半球の主応力方位である.しかし,主応力方位は逆方位の上半球の主応力方位と対になっている.下半球の主応力軸方位について親指をP軸・人差し指をT軸・中指をN軸とすれば,「手系」が右か左かを判定できる.発震機構回転角を算出する場合には,基準の発震機構の手系と比較する発震機構の手系を一致させる必要がある.手系の変換は,一つの主応力軸方位について逆方位の上半球軸方位を用いることによって達成できる.
注2]回転角符号の高角不定
発震機構回転角が90°になると,島弧側回転(正)でも海溝側回転(負)でも同じ発震機構になる.従って,±80°を越す回転角の場合には符号決定が困難になる.今回の解析結果で余震は海溝側回転(負)と述べたが,厳密には,余震4の+89.7°と余震6の+83.9°の2個の余震が正符号を持つ.しかし,その前後の±80°以内の回転角を持つ余震で符号が負なので,負回転と判定し,-90.3°と-96.1°とした.本震判定に重要な役割を担った最大前震から本震までの前震の最大回転角は,80°以内の+74.3で符号決定に問題はない.
注3]オイラー回転極算出法(新妻,2010a)
基準と比較する地震の対応する二つの主応力軸,例えばP軸とT軸,P0・T0とP1・T1の方位と傾斜が与えられれば,オイラー極の位置を算出できる(図142).ここではxyz三次元空間のデカルト座標を用いて算出する.球の中心を原点とし,原点と傾斜0°方位0°を通る軸をx軸,傾斜0°方位90°を通る軸をy軸,下方への軸をz軸とし,球の半径を1とすると,傾斜φP・方位λPの主応力軸Pが球面と交わる点を三次元デカルト(Cartesian)座標でP(xP,yP,zP)とすると,
xP = cosλP cosφP
yP = sinλP cosφP 4_1
zP = sinφP
と算出できる.ここに算出されたxP・yP・zPをPの方向余弦とも呼ぶ.
P0とP1が重なり合うように回転できる回転の中心点がオイラー極(Euler Pole)である.従って,P0とP1はオイラー極から等距離になければならず,オイラー極はP0とP1から等距離にある.P0とP1から等距離の点は三次元空間では,P0とP1を結ぶ直線の垂直二等分面上にあり,T0とT1についてもT0とT1を結ぶ直線の垂直二等分面上にある.P軸とT軸について等距離の条件を共に満たすのは垂直二等分面の交線であり,オイラー回転の軸になる.
P0(xP0,yP0,zP0)、P1(xP1,yP1,zP1)とすると,直線P0P1の方向に直交し、球の中心を通る垂直二等分面は,ヘッセ(Hess)の標準形で
(xP1 – x P0)x+(yP1 – y P0)y+(zP1 – z P0)z= 0 4_2
と書ける.直線T0T1の方向に直交し、球の中心を通る垂直二等分面の式
(xT1 – xT0)x+(yT1 – y T0)y+(zT1 – z T0)z= 0 4_3
に代入し,変数tを用いて球の中心を通るx・y・zについての交線の式,
|yP1 – y P0 yT1 – y T0|
x = t | | = t ((yP1 – y P0 )(zT1 – z T0) – (yT1 – y T0)(zP1 – z P0))
|zP1 – z P0 zT1 – z T0|
|zP1 – z P0 zT1 – z T0|
y = t | | = t ((zP1 – z P0)(xT1 – x T0) – (zT1 – z T0)( xP1 – x P0)) 4_4
|xP1 – x P0 xT1 – x T0|
|xP1 – x P0 xT1 – x T0|
z = t | | = t ((xP1 – x P0)(yT1 – y T0) – (xT1 – x T0)(yP1 – y P0))
|yP1 – y P0 yT1 – y T0|
を導ける.これらの式の比を取れば変数tは相殺されるので,x/zおよびy/zが算出される.
交線と半径=1の球面との交点については,
x2+y2,+z2=1 4_5
が成り立つ.z≠0として式4_5の両辺をz2で除せば,
x2/z2 + y2/z2 + 1 = 1/z2 4_6
と書き換えられ,さらに
z= ±1/√[(x/z)2 + (y/z)2 + 1] 4_7
が得られる.式4_4から算出されるx/zおよびy/zを式4_7に代入するとzが算出され,x・yも算出できる.交線は球面と2点で交わるが,正負のzがこの2点に対応する.
これらの算出座標がオイラー極の三次元座標E(xE,yE,zE)になる.オイラー極の傾斜φE・方位λEは,
φE = sin-1 ( zE ) 4_8
λE = tan-1 (yE /xE )
によって算出できる.xEが負の場合には算出されるλEに180°を加算する.
算出されたオイラー極の回りをP0およびT0がP1とT1に回転する方向が球の外側から見て左回り(反時計回り)になる点が,算出するオイラー極である.
補注4] 主応力方位テンソルによるオイラー回転極算出法(2015年6月19日追加)
注3]では2組の主応力方位を用いて球面幾何学に基づきオイラー回転を算出し,使用する主応力の組み合わせを変えて算出した各主応力軸のオイラー回転角差が小さなオイラー極を選択して使用していた.しかし,主応力方位テンソルを用いれば3つの主応力軸方位からオイラー回転を算出できるので,算出法を示す.
テンソルD0に回転Rを加えてD1に変化した場合,テンソル演算では,
D1 = RD0
と記述される.D0が基準主応力方位テンソルでD1が比較主応力方位テンソルになり,Rの回転テンソルからオイラー回転を算出するのが本特報の目的である.D0の行と列を入れ換えた逆テンソルをD0-1と記し,両辺に右からD0-1を乗ずると,D0 D0-1=1であるので
D1 D0-1= R D0 D0-1= R
となり,比較テンソルD1に右から基準逆テンソルD0-1を乗ずると回転テンソルRを算出できる.
主応力方位から基準と比較の方位テンソルD0とD1を算出できれば,回転テンソルRを算出できる.方位テンソルは主応力軸方位の方向余弦を要素とするテンソルであり,
|xP1 xN1 xT1|
D1 = | yP1 yN1 yT1 |
| zP1 zN1 zT1 |
と表され,逆モーメントテンソルは行と列を入れ換えて,
|xP0 yP0 zP0 |
D0-1= | xN0 yN0 zN0 |
| xT0 yT0 zT0 |
と表される.従って,
|xP1 xN1 xT1| |xP0 yP0 zP0 |
R = D1 D0-1 =| yP1 yN1 yT1 | | xN0 yN0 zN0 |
|zP1 zN1 zT1 | | xT0 yT0 zT0 |
| xP1 xP0+ xN1 xN0+ xT1 xT0 xP1 yP0+ xN1 yN0+ xT1 yT0 xP1 zP0+ xN1 zN0+ xT1 zT0 |
= | yP1 xP0+ yN1 xN0+ yT1 xT0 yP1 yP0+ yN1 yN0+ yT1 yT0 yP1 zP0+ yN1 zN0+ yT1 zT0 |
| zP1 xP0+ zN1 xN0+ zT1 xT0 zP1 yP0+ zN1 yN0+ zT1 yT0 zP1 zP0+ zN1 zN0+ zT1 zT0 |
回転テンソルRとオイラー回転の関係はx,y,z軸の周りの回転の重ね合わせによって得られる(新妻,2010b).求められた3行3列の回転テンソルRのi行j列の要素をrijすると,オイラー回転角αは,
r11 + r22 + r33 = 1 + 2 cosα
の関係から算出できる.オイラー極の方向余弦xE,yE,zEは,
xE = ( r32 – r23 ) / (2 sinα)
yE = ( r13 – r31 ) / (2 sinα)
zE = ( r21 – r12 ) / (2 sinα)
によって算出できる.
引用文検
新妻信明(2010a)オイラーの定理.「プレートダイナミクス入門」,第2章,共立出版,31-41.
新妻信明(2010b)プレート運動と回転テンソル.「プレートダイナミクス入門」,付録II,共立出版,109-120.